
Lenet-5 识别手写数字
一、实验要求
本次实验,我们需要实现一个基于Lenet-5神经网络模型的手写数字识别系统。同时,使用MNIST数据集进行训练和测试。
Lenet-5
首先简要介绍一下Lenet-5模型。
LeNet-5模型是一个十分经典的卷积神经网络模型,最早由Yann LeCun教授于1998年在其论文《Gradient-Based Learning Applied to Document Recognition》中提出。作为首个成功应用于数字识别任务的卷积神经网络,LeNet-5在MNIST数据集上的准确率约为99.2%。该模型的提出标志着卷积神经网络在计算机视觉领域的应用取得了重要进展。
模型架构
Lenet-5模型共有7层(不计输入层),每层均包含可训练参数。模型架构如下图所示。
下面对架构进行逐层讲解。
输入层
输入层所输入的图片大小应为32*32,略大于MNIST数据集中图片大小(28*28),因此需要为输入图像加上宽度为2的padding。这么做是因为我们希望在第一层卷积层(卷积核5*5)进行卷积时,将原输入图片中的所有数据保持在特征检测子感受野(receptive field)的中心。
C1层
C1层为卷积层,使用6个5*5的卷积核进行卷积,步长为1,得到6个28*28的特征图。
S2层
S2层为池化层,采用最大池化,池化大小为2*2,得到6个14*14的特征图。
在原论文中,Lecun教授采用的是平均池化的方法进行池化,但在后人进一步探索的过程中,发现采用最大池化效果更佳,因此目前的Lenet-5模型的池化层都普遍采用最大池化。
C3层
C3层为卷积层,使用16个5*5的卷积核进行卷积,步长为1,得到16个10*10的特征图。
S4层
S4层为池化层,采用最大池化,池化大小为2*2,得到16个5*5的特征图。
C5层
C5层较为特殊。在设计中,C5层为一个卷积层,使用120个5*5,步长为1的卷积核进行卷积。因此,这一层最终会得到120个大小为1*1的特征图,这其实就相当于一个全连接层。但在实现时,最好依旧将其设为卷积层而非全连接层,以保证对于其它大小的输入数据(如64*64的图像输入),模型具有相同的结构。
F6层
F6层为全连接层,输出大小为84。
输出层
输出层与F6层全连接,输出长度为10的张量,指示最终的预测结果。
下面是模型各层参数的汇总表格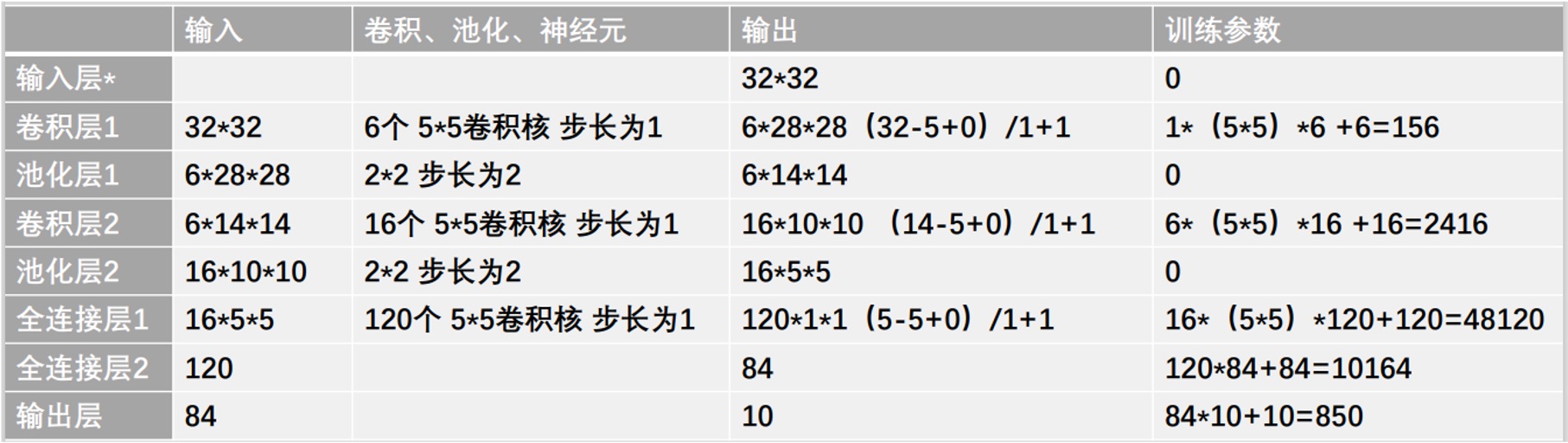
二、算法设计
对于这次实验,不需要做过多算法设计上的工作,只需成功将模型复现,并使用MNIST数据集进行训练和测试即可。
这次使用pytorch进行实现,代码主要分为5个模块,分别为
- 数据加载模块
- 模型定义模块
- 训练模块
- 测试模块
- 展示demo
下面进行详细阐述。
数据加载模块
由于pytorch中已经定义了MNIST数据集的相关处理函数,因此只需直接将其导入即可,只需配置几个参数便能完成数据集的导入。
在MNIST数据集中存在训练用数据和测试用数据两个测试文件,我们在导入时将train设为True即可使用训练集,而设为False即可使用测试集。同时,如果指定下没有MNIST数据集,通过将download设为True可以直接进行下载。
随后,还需要创建对训练数据和测试数据的数据加载器,用于批量加载多组数据。对于训练数据,每次加载的数据量需要谨慎选择,因为其会影响模型最终的学习效果,在这里我们选择较为常用且大小合适的数据量128。而对于测试集,则不会对最终的测试结果产生影响,考虑到测试集数据总量为10k,在这里我们就选择100作为数据加载量。
同时,对于训练数据,我们应该在每加载一轮后对数据进行洗牌,使数据随机重新排列,以避免数据的顺序对模型的学习产生影响,通过将shuffle设为True即可完成这一操作。测试数据则不需要洗牌。
模型定义模块
对于模型定义部分,只需按照前面给出的模型架构逐层进行定义即可。需要注意的是,在前向传播函数中,C5层的每个卷积核计算完毕后得到的数据是一个1*1的二维向量,还需要将其展平为一维后才能输入F6全连接层进行计算。
此外,还应定义并对每层的输出使用激活函数,已获得更好的训练效果。在这里使用的激活函数十分简单但也十分经典,如果输入x大于0就输出x,否则输出0,用于丢弃所有前向传播过程中的负值。
具体代码如下。
1 | # LeNet-5模型架构定义 |
训练模块
对于训练模块,我们首先需要定义损失计算函数和优化器。损失计算函数此处使用比较经典的交叉熵损失函数,而优化器也使用经典的Adam优化器,初始学习率设为0.001。
随后,将模型设置为训练模式,便可以开始使用训练数据集进行训练,训练按如下流程进行。
- 加载训练数据,并将数据输入模型中进行运算
- 得到模型运算结果,将结果和数据标签传入损失函数,计算损失
- 根据损失对模型进行反向传播,计算各连接的梯度
- 通过优化器和前面计算得到的梯度对模型进行参数更新
- 实时输出训练进度和损失值
在训练中,需要注意每训练完一组数据后需要对模型进行梯度清零,以避免前面的数据影响后续数据的训练效果,进而导致过拟合等问题。此外,在多次迭代训练的情况下,我采用了学习率梯度下降的训练方式,每十次迭代下降1/10,以提高高次迭代下的训练效果。
对于实时进度输出,可以通过在每行输出后添加end='\r'的方式清除上一条输出,以实现输出实时变化的效果,并可以据此制作实时进度条,十分有趣。
最后,我们需要将训练完毕的模型进行保存,以便后续测试和演示使用。
此模块部分代码如下。Training Module 1
2
3
4
5
6
7
8
9
10
11
12
13
14# 训练模块
def train(epoch):
model.train() # 设置模型为训练模式
process = 0
if epoch % 10 == 0: # 每10个训练周期,学习率梯度下降至原来的0.1
for param_group in opt.param_groups:
param_group['lr'] *= 0.1
for batch_index, (data, target) in enumerate(train_loader):
data, target = Variable(data), Variable(target)
opt.zero_grad() # 梯度清零
output = model(data) # 前向传播
loss = loss_counter(output, target) # 计算损失
loss.backward() # 反向传播,计算梯度
opt.step() # 更新模型参数
测试模块
对于测试模块,与前面的训练模块类似,首先将模型设为训练模式,随后读入数据并传入模型进行计算,再根据计算结果与标签进行对比,获得损失。但并不执行反向传播和参数更新这两项操作,而是将通过将计算结果转化为预测结果,再将标签进行对比来判断模型预测结果的正误。统计每组测试数据的预测正确性和所有数据的平均损失,也将其实时输出,以查看模型的正确率。
在预测结果的判断上,我们只需先取得模型的输出(10维张量),从中寻找值最大的一个分量,该分量的下标即是模型所预测的数字。
下面是此部分代码。
1 | # 测试模块 |
演示demo
此模块主要实现实时测试的功能,即不使用MNIST数据集,通过手动写入数据,运行模型并输出预测结果,以起到演示模型效果的作用。
出于简单考虑,这里不手动输入28*28的矩阵,而是输入一个7*7的矩阵,再将其等比扩展4倍,即可得到28*28的矩阵。
随后,只需将矩阵输入至模型,计算结果并得到模型的预测结果,再将其输出即可。同时,输出还包括最初输入矩阵的更清晰表示,以便使用者更好的查看,以及模型输出的十维张量,以对模型计算结果有更清晰的了解(为了输出美观考虑,此处作为整数输出,实际结果应为浮点数)。
但需要注意,这种测试方法十分简陋,因此测试时尽量输入特征明显的数字作为输入,且演示结果并不能很好的反应模型实际性能,只能作为一种简单有趣的演示。
此模块部分代码如下。
1 | def demo(): |
三、程序测试
我分别训练了迭代次数为1、5、10、15、20、25、30、40、50的模型,并对其进行了测试,得到了迭代次数与测试正确率关系如下:
1 | 1: 96.69% |
可以看到,25次迭代下的模型效果最佳,正确率可以达到99.2%以上,与最初的预期相符。此外,迭代次数大于20后模型的整体表现均不错,且在更高迭代次数下正确率保持稳定,没有出现数据过拟合而导致效果下降的问题。
最后,我还用演示模块进行了几次测试,结果如下。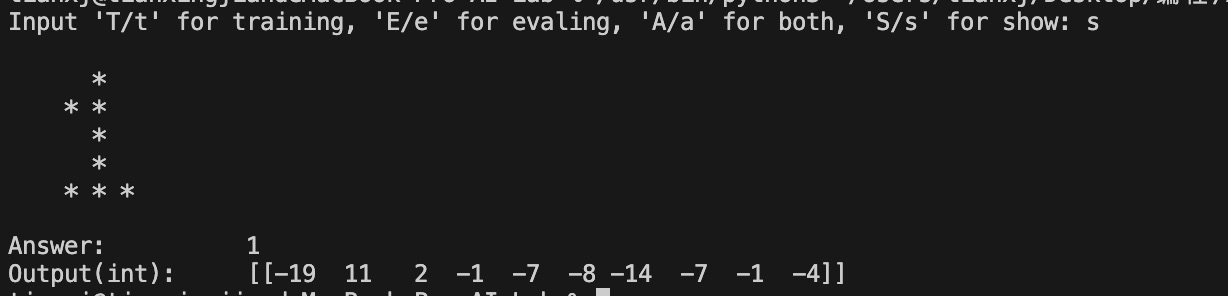
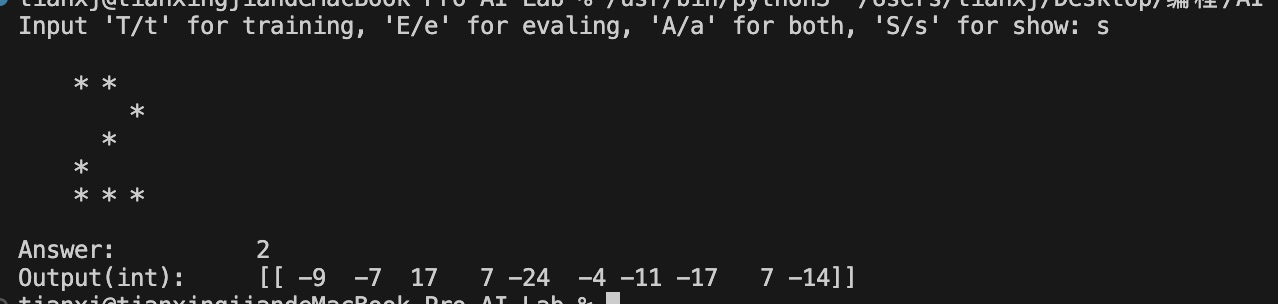
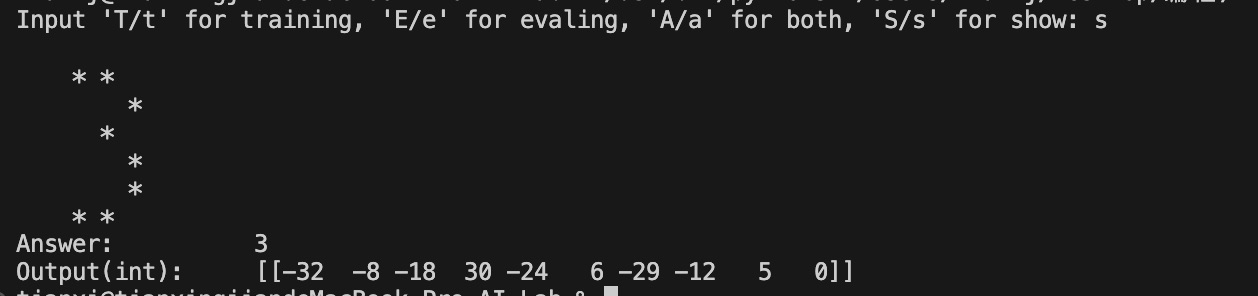
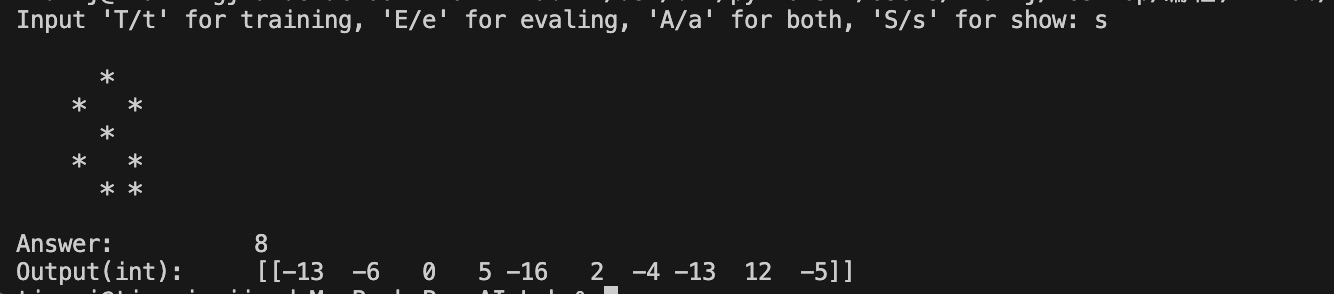
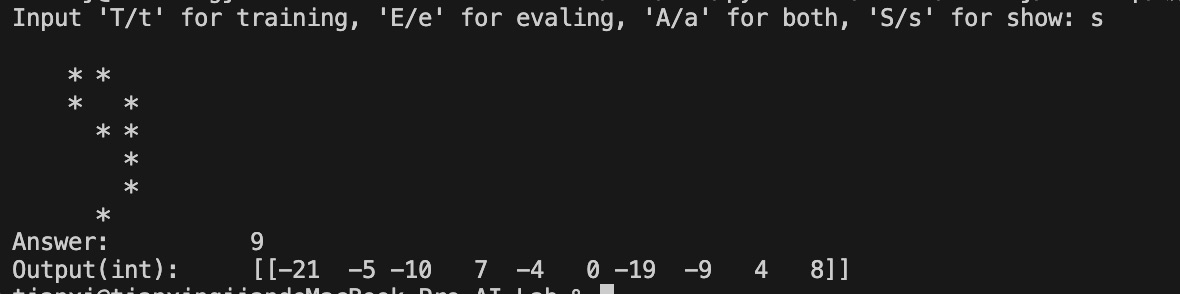
四、实验总结
这次实验还比较有趣,了解并复现了一个经典的卷积神经网络,并且通过实验的机会初步认识学习了pytorch。由于实验要求中并没有给出很多模型的复现细节,例如激活函数、损失函数、优化器、学习率设置等,因此在实验过程中需要自己不断的探索,分析和调参,以得到一个不错的模型效果,过程虽然有些煎熬和枯燥,但最终得到不错的结果时还是很开心的。
五、源码
这次实验稍显复杂,就不给源码了
- Title: Lenet-5 识别手写数字
- Author: 梦猫
- Created at : 2024-05-26 18:37:27
- Updated at : 2024-05-28 10:56:04
- Link: https://mengmaor.github.io/2024/05/26/Lenet-5-识别手写数字/
- License: All Rights Reserved © 梦猫

